RANGKAIAN SERI DAN PARALEL

Sebuah rangkaian seri dengan sumber tegangan dan 3 resistor

Komponen sebuah rangkaian listrik atau rangkaian elektronik dapat dihubungkan dengan berbagai cara. Dua tipe paling sederhana adalah rangkaian seri dan parallel. Rangkaian yang disusun secara sejajar disebut rangkaian seri, sedangkan rangkaian yang disusun secara berderet disebut rangkaian paralel. Komponen yang tersusun seri akan terhubung melalui satu jalur, sehingga aliran arus listrik akan mengalir ke semua komponen.[1][2] Pada rangkaian paralel, tegangan yang melewati tiap komponen adalah sama, dan total arus adalah jumlahan arus yang melewati tiap komponen.[1]

Anggap sebuah rangkaian sederhana yang terdiri dari 4 lampu dan satu baterai 6 V. Jika keempat lampu terhubung seri, maka arus yang melewati tiap lampu sama dan voltage drop turun 1.5 V setiap lampu, yang mungkin tidak cukup untuk menyalakan semua lampu. Jika keempat lampu terhubung paralel, arus yang melalui tiap lampu akan digabungkan, sedangkan voltage drop turun melalui tiap lampu dan semuanya bisa menyala.

Rangkaian listrik paralel adalah suatu rangkaian listrik, di mana semua input komponen berasal dari sumber yang sama. Semua komponen satu sama lain tersusun paralel. Hal inilah yang menyebabkan susunan paralel dalam rangkaian listrik menghabiskan biaya yang lebih banyak (kabel penghubung yang diperlukan lebih banyak). Selain kelemahan tersebut, susunan paralel memiliki kelebihan tertentu dibandingkan susunan seri. Adapun kelebihannya adalah jika salah satu komponen dicabut atau rusak, maka komponen yang lain tetap berfungsi sebagaimana mestinya

Gabungan antara rangkaian seri dan rangkaian paralel disebut rangkaian seri-paralel (kadang disebut sebagai rangkaian campuran atau rangkaian kombinasi).


{\displaystyle I=I_{1}=I_{2}=I_{3}=\dots =I_{r}}

Pada rangkaian seri, arus yang lewat besarnya sama tiap elemen.


Resistor[

Total hambatan resistor pada rangkaian seri sama dengan jumlahan masing-masing hambatan:

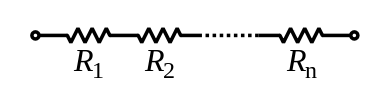{\displaystyle R_{\text{total}}=R_{1}+R_{2}+\cdots +R_{n}}



Konduktansi listrik berkebalikan dengan hambatan. Total konduktansi pada rangkaian seri dari resistor dapat dihitung dari persamaan berikut:{\displaystyle {\frac {1}{G_{\mathrm {total} }}}={\frac {1}{G_{1}}}+{\frac {1}{G_{2}}}+\cdots +{\frac {1}{G_{n}}}}.

Untuk kasus khusus dengan 2 resistor dipasang seri, total konduktansi sama dengan:{\displaystyle G_{\text{total}}={\frac {G_{1}G_{2}}{G_{1}+G_{2}}}.}
Induktor

Induktor juga mengikuti hukum yang sama:

{\displaystyle L_{\mathrm {total} }=L_{1}+L_{2}+\cdots +L_{n}}

Namun, dalam beberapa kasus sulit untuk menghindari induktor yang berdekatan untuk saling mempengaruhi, karena medan magnet dari satu elemen akan terhubung dengan elemen lainnya. Pengaruh ini didefinisikan pada induktansi-saling M. Jika 2 induktor dipasang seri, ada kemungkinan besarnya induktansi sama tergantung dari medan magnet dari kedua induktor mempengaruhi satu sama lain.
Kapasitor
Kapasitor mengikuti hukum berkebalikan. Total kapasitansi yang dipasang seri sama dengan dari jumlah kebalikan masing-masing elemen:

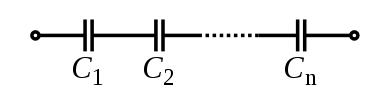{\displaystyle {\frac {1}{C_{\mathrm {total} }}}={\frac {1}{C_{1}}}+{\frac {1}{C_{2}}}+\cdots +{\frac {1}{C_{n}}}}.
Rangkaian paralel

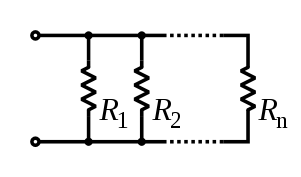{\displaystyle {\frac {1}{R_{\mathrm {total} }}}={\frac {1}{R_{1}}}+{\frac {1}{R_{2}}}+\cdots +{\frac {1}{R_{n}}}}.Jumlah kebalikan hambatan total rangkaian paralel sama dengan jumlah dari kebalikan hambatan tiap- tiap komponen (resistor).
Catatan
^ a b Resnick et al. (1966), Chapter 32, Example 1.
^ Smith, R.J. (1966), page 21